A finite state machine is an automaton that can recognize regular grammars (regular expressions).
Deterministic Finite Automata (DFA)
A DFA contains the following elements:
- A finite set of states, commonly denoted as $Q$
- A finite set of input symbols, commonly denoted as $\Sigma$
- A state transition function that takes a state (call it $B$) and an input symbol (call it $a$) as parameters and returns a state (call it $C$), representing that when the machine is in state $B$ and receives input $a$, it should transition to state $C$. This is commonly denoted as $\delta$, written as $C = \delta(B, a)$
- An initial state, commonly denoted as $q_0$, where $q_0 \in Q$
- A set of final or accepting states, commonly denoted as $F$, where $F \subseteq Q$
A DFA is commonly represented as a 5-tuple of these elements, written as $A = (Q, \Sigma, \delta, q_0, F)$
Nondeterministic Finite Automaton (NFA)
An NFA extends a DFA by changing the state transition function to return a set of states rather than a single state, and allowing the empty string $\epsilon$ as an input symbol.
NFA Determinization
An NFA can be converted to an equivalent DFA.
Example
Let's start with an example:
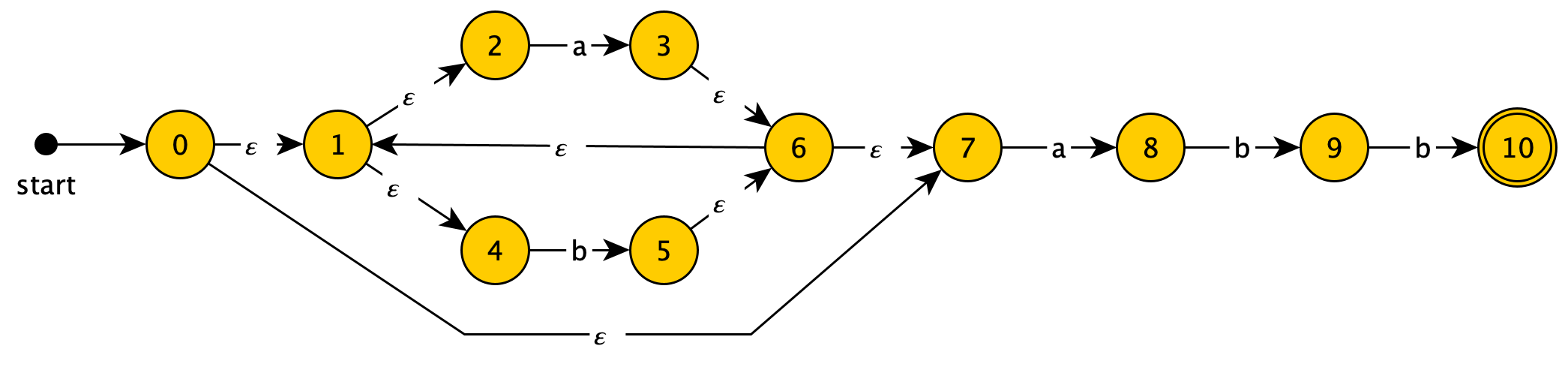
This NFA recognizes $(a|b)*abb$.
We'll convert this NFA to a DFA.
Starting from the start state, even without any input, from state $0$ we can reach states ${0,1,2,4,7}$ via $\epsilon$ transitions. Since DFAs don't have $\epsilon$ transitions but must have a start state, in our generated DFA these states must be combined into a single state, which we'll call $A$.
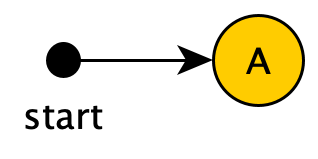
Next, let's look at which states we can reach from state $A$ (which represents NFA states ${0,1,2,4,7}$) with input $a$:
- From $2$, we can reach $3$
- From $7$, we can reach $8$
- From states $3$ and $8$, we can reach ${1,2,3,4,6,7,8}$ via $\epsilon$ transitions
So after input $a$ from state $A$ in the original NFA, we can reach NFA states ${1,2,3,4,6,7,8}$. This combination is clearly not state $A$, so we'll create a new state $B$ and connect it after $A$:
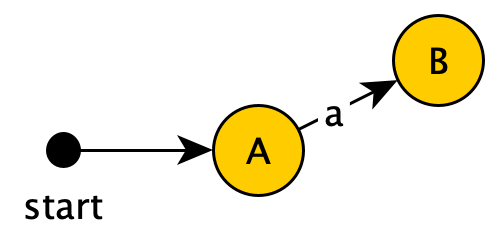
Similarly for input $b$ from state $A$:
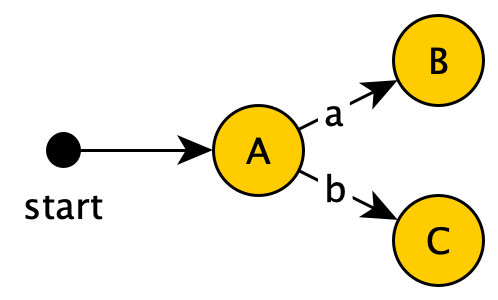
We've now examined all paths from state $A$ in the DFA.
For clarity, I've annotated the corresponding NFA states on the DFA diagram:
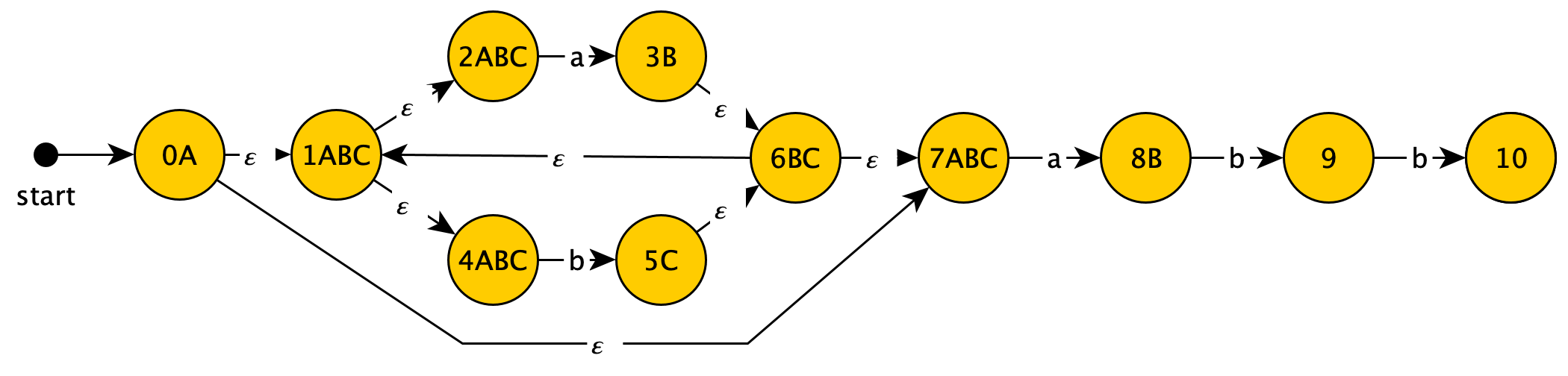
Let's continue examining from state $B$:
- From this state via $a$, we can reach states ${1,2,3,4,6,7,8}$, which takes us back to $B$, so $B$ transitions to itself on input $a$
- From this state via $b$, we can reach states ${1,2,4,5,6,7,9}$, which is a new combination of NFA states, so we'll create a new DFA state $D$
This gives us:
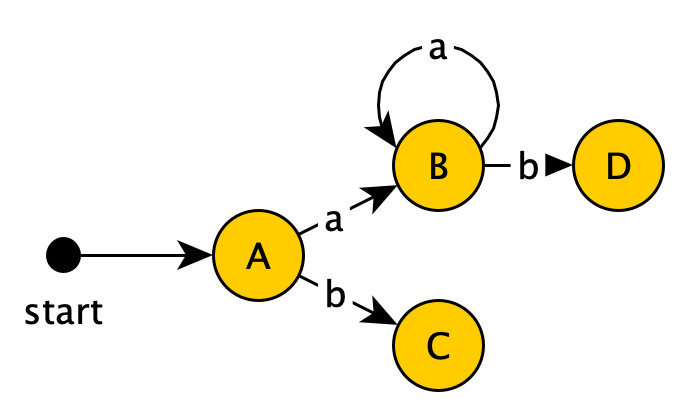
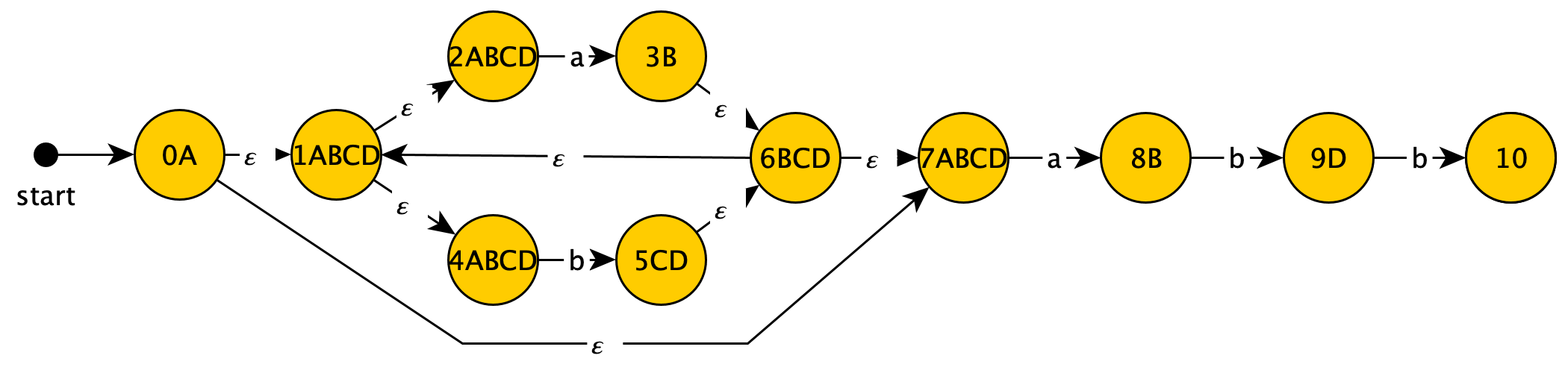
Next examining state $C$:
-
$C+a \rightarrow {1,2,3,4,6,7,8}$, which takes us to $B$
-
$C+b \rightarrow {1,2,4,5,6,7}$, which takes us back to $C$
So:
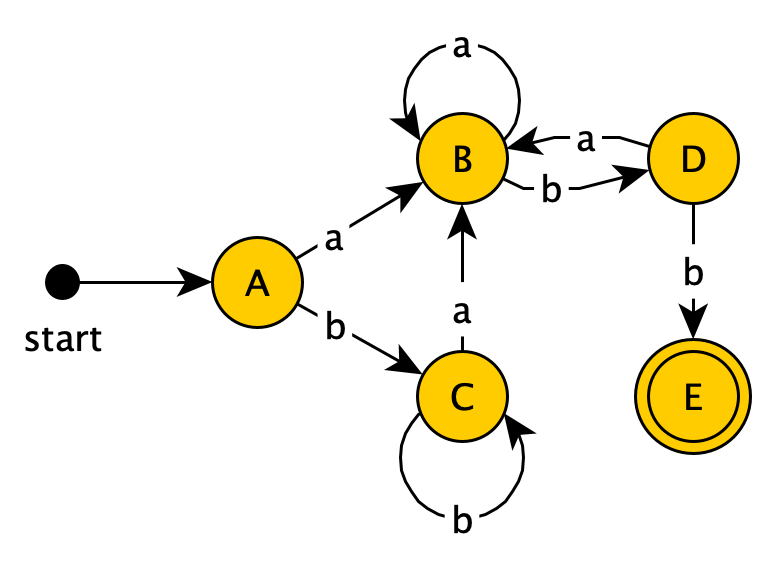
Then state $D$:
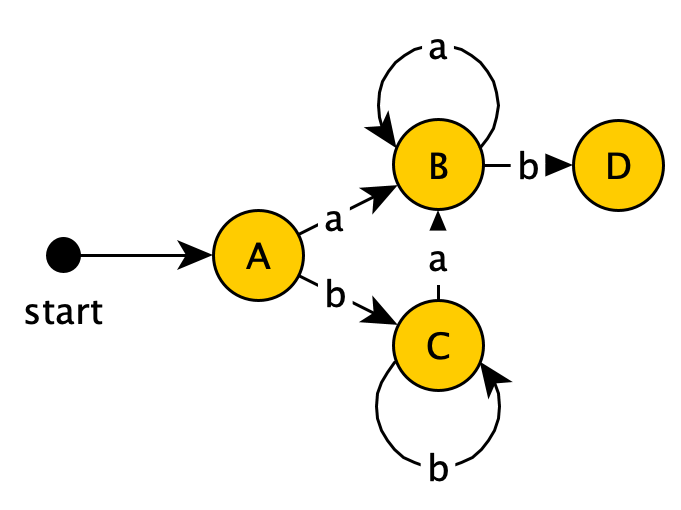
- $D+a \rightarrow {1,2,3,4,6,7,8}$, which takes us to $B$
- $D+b \rightarrow {1,2,4,5,6,7,10}$, creating new state $E$. Since $E$ contains the accepting state $10$ from the original NFA, it becomes an accepting state in the DFA.
This gives us:

Finally, for state $E$:
- $E+a→B$
- $E+b→C$
So we get:
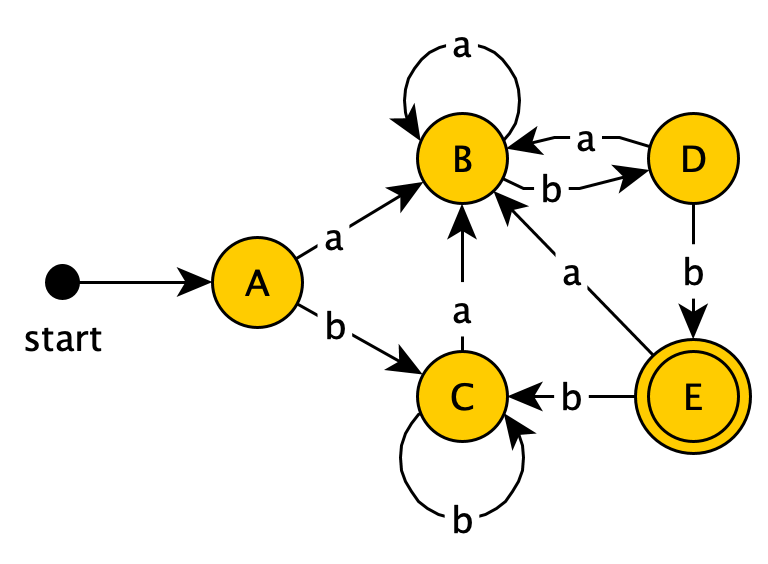
Since all states in this DFA have been examined, this is our final result.
Here's the final mapping table from NFA states to DFA states:
| NFA | DFA |
|---|---|
| 0,1,2,4,7 | A |
| 1,2,3,4,6,7,8 | B |
| 1,2,4,5,6,7 | C |
| 1,2,4,5,6,7,9 | D |
| 1,2,4,5,6,7,10 | E |
Algorithm
Summarizing the above process, we can derive the NFA determinization algorithm:
- Map the NFA's start state and all states reachable via $\epsilon$ transitions to the DFA's start state
- If all states in the DFA have been "examined", the algorithm is complete
- Otherwise, consider an unexamined state $N$ in the DFA:
- For each symbol $ch$ in the alphabet
- Find the set of all states reachable from this node's corresponding NFA states via $ch$ and any number of $\epsilon$ transitions
- If this set is a subset of the NFA states corresponding to an existing DFA state $M$, add a transition $N + ch = M$
- Otherwise add a new DFA state $P$ corresponding to this set of NFA states. If this set contains an accepting state, make this node an accepting state, and add the transition $N+ch=P$
- The resulting DFA is the solution
Code
Code available in the Github repository.
fun toDFA(): Deterministic {
start as Nondeterministic.State
// States not yet examined, equivalentStates: states reachable via ε transitions
// Since DFA states aren't fully constructed yet, storing them can be difficult
// So we store the corresponding set of NFA states
val statesToFind = mutableSetOf(start.equivalentStates())
// Transition relation table for result
val result = mutableMapOf<Set<Nondeterministic.State>, Deterministic.State>()
var nextChar = 'A'
// Construct DFA start state
result[start.equivalentStates()] = Deterministic.State(
nextChar++.toString(),
start.equivalentStates().any { it.accept },
mutableMapOf())
while (!statesToFind.isEmpty()) {
// Now consider this set of NFA states corresponding to a DFA state
val theStates = statesToFind.first()
statesToFind.remove(theStates)
for (ch in alphabet) {
val canGoTo = theStates.directConnectedTo(ch)
val equivalenteStates = canGoTo.equivalentStates
// If corresponding DFA state doesn't exist, construct it
if (equivalenteStates !in result.keys) {
result[equivalenteStates] = Deterministic.State(nextChar++.toString(), equivalenteStates.any { it.accept }, mutableMapOf())
statesToFind.add(equivalenteStates)
}
// Add transition from this state to other states
result[theStates]!!.transitions[ch] = result[equivalenteStates]!!
}
}
// Save as DFA and return
return Deterministic(result.values.toSet(), result.values.minBy { it.name }!!)
}
