本文假设读者知道什么是 Hoare Logic。
为什么 Hoare Logic 不够
假设我们有了下面两段程序:
while n != 0 {
r *= n;
n -= 1;
}
和
z += z;
我们可以写出两者的 pre 和 post condition:
// r = 1 && n >= 0 && n = n0
while n != 0 {
r *= n;
n -= 1;
}
// r = n0!
// z = z0
z += z;
// z = 2 * z0
然而,如果我们把两段程序合并起来,整体的 pre 和 post condition 并非是两者的简单合并:
// r = 1 && n >= 0 && n = n0 **&& z = z0**
while n != 0 {
r *= n;
n -= 1;
}
// r = n0! **&& z = z0**
// z = z0 **&& z = z0**
z += z;
// z = 2 * z0 **&&r = n0!**
可见,我们必须将一些和局部变量无关的断言加入 pre 和 post condition,也就是说,任何局部变量的 pre 和 post condition 都影响整体。
分离逻辑
为了区分程序中的局部和整体,我们将 Hoare Logic 中的 pre 和 post condition 中的 conjunction($\wedge$)改为 separating conjunction ($*$)。
同时将 Hoare Logic 中由变量取值构成的上下文分为 由局部变量取值构成的上下文 和 由全局变量构成的堆。
堆
类似 C 语言中的堆,就是吧一个地址映射到一个值。
符号记作 $[a_1 \mapsto v_1, a_2 \mapsto v_2, \dots]$。
断言
分离逻辑中的断言写作:
$$ s, h \models e $$
表示给定状态 $s$ 和堆 $h$,$e$ 成立。
其中 $e$ 形如:
- $p ∨ q$,意为 $s, h \models p$ 或 $s, h \models q$;
- $∃v . p(v)$,意为存在 $v$,使得 $s, h \models p(v)$;
- $\text{emp}$,意为 $h$ 为空(所有地址上的值都是 undefined);
- $e_1 \mapsto e_2$,意为 $h = [E(e_1, s) \mapsto E(e_2,s)]$,$E$ 指在某个条件(这里是 $s$)下 evaluate 。
- $p * q$,意为 $h$ 可以被分割为不相交的两个部分 $h_1$ 和 $h_2$,使得 $s, h_1 \models p$ 且 $s, h_2 \models q$;
- $\langle p \rangle$,意为 $p(s)$ 且 $h$ 为空,几个有趣的结论是 $\langle true \rangle = emp$, $\langle b1\rangle * \langle b2 \rangle = \langle b1 \land b2 \rangle$。
对堆进行的操作
我们用 $[E]$ 代表对堆中地址 $E$ 处的元素的引用。
用 cons(init_0, init_1, ..., init_n) 在堆中 allocate 一些空间,其中元素的值为 $init_0, init_1, ..., init_n$。
用 dispose(E) 来 丢弃地址 $E$ 处的元素。
证明
Rules
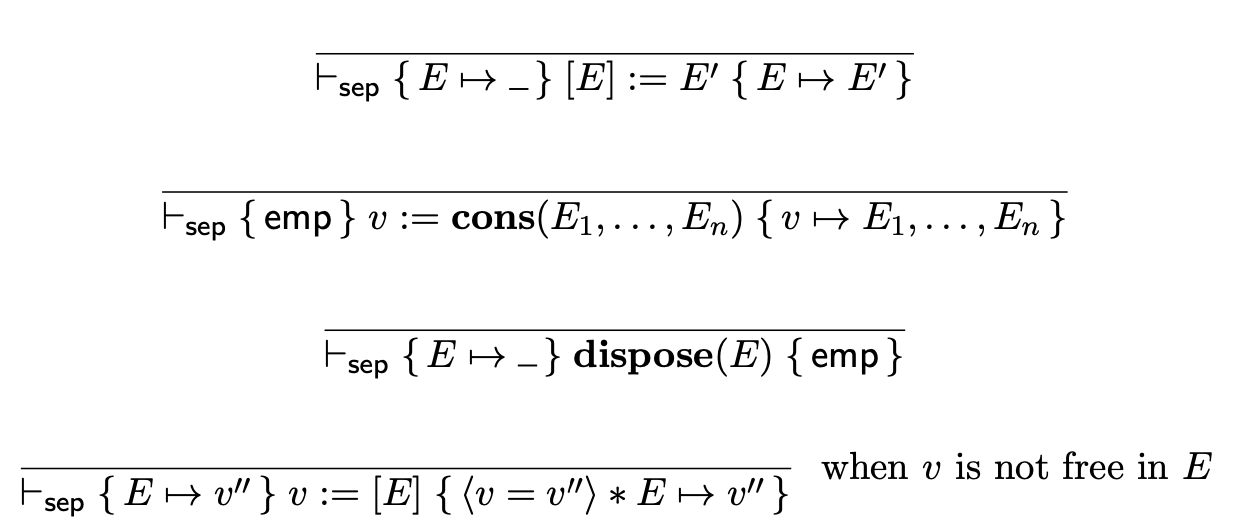
- Frame Rule: $$ \require{bussproofs} \begin{prooftree} \AxiomC{$⊢ \{P\} C \{Q\}$} \UnaryInfC{$⊢ \{P*R\} C \{Q*R\}$} \end{prooftree} $$ 其中 C 没有修改 R 中的相关内容。
例子
$$ \vdash \{emp\}\ x := cons(0); y := cons(x); [x] := y\ \{ x → y * y → x \} $$
证明:
$$ \tag{1} ⊢ \{emp\} x := cons(0); \{x \mapsto 0\} $$ $$ \tag{2} ⊢ \{emp\}\ y := cons(x);\ \{y \mapsto x\} $$ $$ \tag{3} ⊢ \{x \mapsto \_\}\ [x] := y;\ \{x \mapsto y\} $$
结合 $(2)$ 和 Frame rule,取 $R = {x \mapsto 0}$,得: $$ \tag{4} ⊢ \{x \mapsto 0\}\ y := cons(x);\ \{y \mapsto x * x \mapsto 0\} $$
结合 $(1)$ 和 $(4)$,得: $$ \tag{5} ⊢ \{emp\}\ x := cons(0); y := cons(x);\ \{y \mapsto x * x \mapsto 0\} $$
再结合 $(3)$ 和 Frame rule,取 $R = {y \mapsto x}$,得: $$ \tag{6} ⊢ \{y \mapsto x * x \mapsto \_\}\ [x] := y;\ \{y \mapsto x * x \mapsto y\} $$
最后结合 $(5)$ 和 $(6)$,得: $$ \vdash \{emp\}\ x := cons(0); y := cons(x); [x] := y\ \{ y \mapsto x * x \mapsto y \} $$ 即为所求证。
