文法
原始递归函数是一种函数式的计算模型,其文法定义如下:
$$ \require{bussproofs} \begin{prooftree} \AxiomC{} \UnaryInfC{$\text{zero} \in \text{PRF}_0$} \end{prooftree} $$
$$ \require{bussproofs} \begin{prooftree} \AxiomC{} \UnaryInfC{$\text{suc} \in \text{PRF}_1$} \end{prooftree} $$
$$ \require{bussproofs} \begin{prooftree} \AxiomC{$i \in \mathbb{N}$} \AxiomC{$0 ≤ i < n$} \BinaryInfC{$\text{proj} \ i \in \text{PRF}_{n}$} \end{prooftree} $$
$$ \require{bussproofs} \begin{prooftree} \AxiomC{$f \in \text{PRF}_{m}$} \AxiomC{$gs \in \text{PRF}_{n}[m]$} \BinaryInfC{$\text{comp} \ f \ gs ∈ \text{PRF}_n$} \end{prooftree} $$
$$ \require{bussproofs} \begin{prooftree} \AxiomC{$f \in \text{PRF}_n$} \AxiomC{$g \in \text{PRF}_{n+2}$} \BinaryInfC{$\text{rec} \ f \ g ∈ \text{PRF}_{n+1}$} \end{prooftree} $$
其中 $\text{PRF}_n$ 中的 $n$ 是一个自然数,代表函数的参数个数。
$PRF_n[m]$ 是一个长度 为 $m$ 的列表(可以由 , 或者任何你喜欢的符号分隔,毕竟文法不重要),其中的元素是 $PRF_n$。
语义
人话语义
每个原始递归函数都接受一个自然数参数列表,并返回一个自然数。
$\text{zero}$ 和 $\text{suc}$ 好理解,不多赘述。
$\text{proj} \ i$ 就是取参数列表中的第 $i$ 个元素。
$\text{comp} \ f \ gs$ 就是先调用 $gs$ 中的每一个函数(使用的就是当前的参数列表),然后用结果作为参数再调用 $f$。 可以理解为 $f$ 和 $gs$ 的复合 $f \circ gs$。
用 JS 表示就是:
const comp = function(f, gs, args) {
return f(...gs.map(g => g(args))));
}
$\text{rec} \ f \ g$ (假设参数列表为 $(n, x_1, x_2, \dots, x_n)$)就是
- 当前结果为 $f(x_1, x_2, \dots, x_n)$
- 将当前结果与调用 $g$ 的次数作为参数,调用 $g$,直到调用 $g$ 的次数达到 $n$ 次。
用 JS 表示就是:
const rec = function(f, g, n, args) {
let result = f(args);
for (let i = 0; i < n; i++) {
result = g(result, i);
}
return result;
}
指称语义
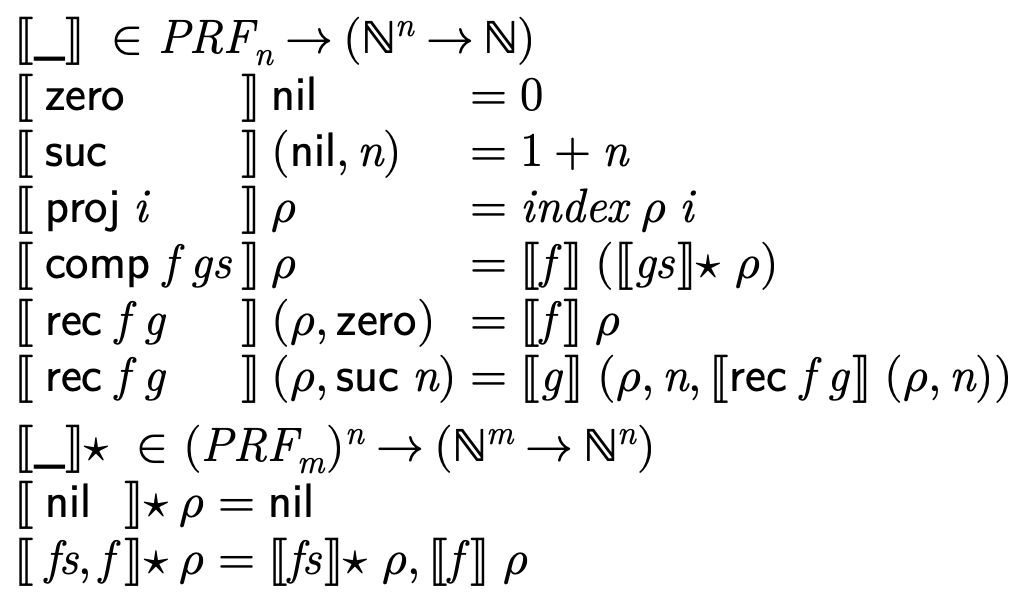
其中 index 定义如下:

注意这里的参数列表是反着写的,不过这只是一个 design choice, 对理解“这是什么”影响不大。
大步 operational 语义

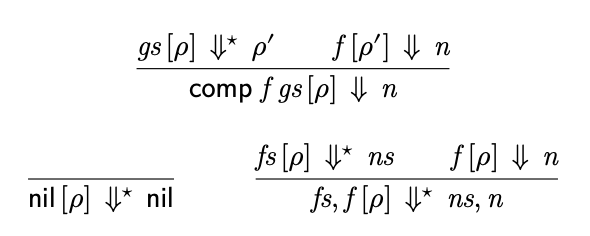
index 定义同上。
计算能力
直觉地,我们可以看出“原始递归函数” 这个计算模型应当能计算 所有 在 固定次数的循环 中能计算出来的 函数的 值。
不能算什么
self-interpreter
我们无法用 原始递归函数 来编写 原始递归函数 的解释器。
形式化地,不存在这样的 原始递归函数 $eval$:
$∀ f ∈ PRF_1, n ∈ ℕ.⟦ eval ⟧ (nil, ⌜ (f, n) ⌝) = ⟦ f ⟧ (nil, n)$
其中 $⌜ (f, n) ⌝$ 是 $f$ 和 $n$ 编码到的自然数。
这个编码方式可以参考 哥德尔数。
我们假设 $(a, b)$ 被编码为 $2^a3^b$。
证明思路是构造 g = comp suc (nil, comp eval (nil, f)),其中 $⟦ f ⟧ (\text{nil}, n) = 2^n3^n$。
我们可以得到 $⟦g⟧ (\text{nil}, \text{code}\ g) = 1 + ⟦g⟧ (\text{nil}, \text{code}\ g)$(其中 code 是将
$PRF_1$ 编码为自然数的函数),这是一个矛盾。
Iterated exponentials
$ \displaylines { ↑ ∈ ℕ → ℕ → ℕ → ℕ \\ 𝑚 ↑^\text{zero}\ 𝑘 = 𝑚𝑘 \\ 𝑚 ↑^{\text{suc}\ n}\ zero = 1 \\ 𝑚 ↑^{\text{suc}\ n}\ \text{suc}\ k = 𝑚 ↑^𝑛 (𝑚 ↑^{\text{suc}\ n}\ 𝑘) } $
Ackermann 函数
ack ∈ ℕ × ℕ → ℕ
ack (zero, n) = suc n
ack (suc m, zero) = ack (m, suc zero)
ack (suc m, suc n) = ack (m, ack (suc m, n))
和其他计算模型的关系
和 PRF 相似,但比 PRF 更弱的计算模型是 elementary recursive function,说实话它并不递归。
和 PRF 相似,但比 PRF 更强的计算模型是 (General)递归函数(一般简称为 RF)。
简单来说,相比 PRF,RF 添加了一个运算 $\text{min}$,用于搜索某个函数在其他参数给定的情况下,关于第一个参数的最小零点, 显然这个运算是一个 partial function,这个零点可能根本不存在。 RF 的计算能力就和图灵机等价了。
PRF 能计算所有算数阶层中 $\Delta_0^0$ 阶层中的公式,原因是 $\Delta_0^0$ 中所有量词都是有界的,通过 rec 我们可以逐个检查每个值。 实际上 PRF 强于 $\Delta_0^0$。
不那么严格的,“只允许使用有界循环”的面向过程程序强于 $\Delta_0^0$, 等于PRF,两者等价的形式化和证明见 Schwichtenberg and Wainer's Proofs and Computations,section 2.5。
