如果你已经理解了移进-归约分析的基本执行流程了,那么你一定会问,我该如何决定某个步骤上应该“移进”还是应该“归约”呢?应该选择哪个推导式来归约呢?如果我们构造的文法和表达式求值一样简单,那手动根据“栈中现有的值”和“下面要输入的值”来判断就可以了,那么如果我们处理的文法比较复杂呢?
举一个经典的表达式文法的例子:
$$ E \rightarrow E+T|T $$
$$ T \rightarrow T*F|F $$
$$ F \rightarrow (E) | \textbf{id} $$
我们来模拟一下匹配字符串 $\textbf{id}*\textbf{id}+(\textbf{id}+\textbf{id})*\textbf{id}$ 的过程,并尝试解释每一步选择移进还是归约的原因。
| 符号栈 | 剩余输入 | 动作 | 原因 |
|---|---|---|---|
| $\textbf{id}*\textbf{id}+(\textbf{id}+\textbf{id})*\textbf{id}$ | 移进 $\textbf{id}$ | 没得选 | |
| $\textbf{id}$ | $*\textbf{id}+(\textbf{id}+\textbf{id})*\textbf{id}$ | 栈顶归约为 $F$ | 下一个符号是$*$,而没有包含 $\textbf{id} *$ 的规则,但栈顶可以归约 |
| $F$ | $*\textbf{id}+(\textbf{id}+\textbf{id})*\textbf{id}$ | 栈顶归约为 $T$ | 下一个符号是$*$,而没有包含$F *$ 的规则,但栈顶可以归约 |
| $T$ | $*\textbf{id}+(\textbf{id}+\textbf{id})*\textbf{id}$ | 移进 $*$ | 下一个符号是$*$, 而没有包含 $ T *$ 的规则 |
| $T*$ | $\textbf{id}+(\textbf{id}+\textbf{id})*\textbf{id}$ | 移进 $\textbf{id}$ | 栈顶不能归约,只能移进 |
| $T*\textbf{id}$ | $+(\textbf{id}+\textbf{id})*\textbf{id}$ | 栈顶归约为 $F$ | 下一个符号是$+$,而没有包含 $T *\textbf{id}+$ 或者 $\textbf{id}+$ 的规则,但栈顶可以归约 |
| $T*F$ | $+(\textbf{id}+\textbf{id})*\textbf{id}$ | 栈顶归约为 $T$ | 下一个符号是$+$,而没有包含$T * F+$ 或者 $F+$ 的规则,但栈顶可以归约 |
| $T$ | $+(\textbf{id}+\textbf{id})*\textbf{id}$ | 栈顶归约为 $E$ | 下一个符号是$+$,而没有包含$T+$ 的规则,但栈顶可以归约 |
| $E$ | $+(\textbf{id}+\textbf{id})*\textbf{id}$ | 移进 $+$ | 栈顶不能归约,只能移进 |
| $E+$ | $(\textbf{id}+\textbf{id})*\textbf{id}$ | 移进 $($ | 栈顶不能归约,只能移进 |
| $E+($ | $\textbf{id}+\textbf{id})*\textbf{id}$ | 移进 $\textbf{id}$ | 栈顶不能归约,只能移进 |
| $E+(\textbf{id}$ | $+\textbf{id})*\textbf{id}$ | 栈顶归约为 $F$ | 下一个符号是$+$,而没有包含 $\textbf{id}+$ 的规则,但栈顶可以归约 |
| $E+(F$ | $+\textbf{id})*\textbf{id}$ | 栈顶归约为 $T$ | 下一个符号是$+$,而没有包含 $F+$ 的规则,但栈顶可以归约 |
| $E+(T$ | $+\textbf{id})*\textbf{id}$ | 栈顶归约为 $E$ | 下一个符号是$+$,而没有 包含 $T+$ 的规则,但栈顶可以归约 |
| $E+(E$ | $+\textbf{id})*\textbf{id}$ | 移进 | 栈顶不能归约,只能移进 |
| $E+(E+$ | $\textbf{id})*\textbf{id}$ | 移进 | 栈顶不能归约,只能移进 |
| $E+(E+\textbf{id}$ | $)*\textbf{id}$ | 栈顶归约为 $F$ | 下一个符号是$)$,而没有 包含 $\textbf{id})$ 的规则,但栈顶可以归约 |
| $E+(E+F$ | $)*\textbf{id}$ | 栈顶归约为 $T$ | 下一个符号是$)$,而没有 包含 $F)$ 的规则,但栈顶可以归约 |
| $E+(E+T$ | $)*\textbf{id}$ | 栈顶归约为 $E$ | 下一个符号是$+$,而没有包含 $T)$ 的规则,但栈顶可以归约 |
| $E+(E+E$ | $)*\textbf{id}$ | 移进 | 栈顶不能归约,只能移进 |
| $E+(E+E)$ | $*\textbf{id}$ | 栈顶归约为 $F$ | 下一个符号是$*$,没有包含 $)*$ 的规则,但栈顶可以归约 |
| $E+F$ | $*\textbf{id}$ | 栈顶归约为 $T$ | 下一个符号是$*$,没有包含 $F*$ 的规则,但栈顶可以归约 |
| $E+T$ | $*\textbf{id}$ | 移进 | 这里是tricky的地方,这里考虑到优先级问题必须移进,这样看来**优先移进,不行了再归约可能是处理优先级问题的方案** |
| $E+T*$ | $\textbf{id}$ | 移进 | 栈顶不能归约,只能移进 |
| $E+T*\textbf{id}$ | 栈顶归约为 $F$ | 没有符号了,往死里归约 | |
| $E+T*F$ | 栈顶归约为 $T$ | 没有符号了,往死里归约 | |
| $E+T$ | 栈顶归约为 $E$ | 没有符号了,往死里归约 | |
| $E$ | 接受 |
这是一个漫长的过程,在这个过程中我们发现:
- 为了处理运算符的优先级,优先进行移进
- 这和我们编写计算器的方式很像
- 在移进会导致栈中不包含某个可以归约的“前缀”时,必须先归约
- 在栈中的内容不同时,要考虑的是否可以归约的部分也不一样
- 例如在处理栈为 $T*$ 和 $E+T*$ 时,其实都只要考虑 $T*$ 的部分就可以了
那么我们可以看一下有哪些方法解决这些问题。
LR(0)项、状态、产生式中的 “$\cdot$” 与LR(0) 状态机
我们从前面的最后一个问题开始着手。
我们看 $E+T*$ 这里,在这种状态下,我们能用来归约的产生式只有 $T \rightarrow T*F$ 一个,会归约到栈顶上多了一个 $T$ 的状态。1
而在 $T*$ 这里,在这种状态下,我们也能用来归约的产生式只有 $T \rightarrow T*F$ 一个,也只会归约到栈顶上多了一个 $T$ 的状态。
可以看出从“往栈上放一个$T$的角度来看”这两个状态其实是同一个状态。
LR(0)项
我们引入$\cdot$标记来分割生成式匹配过了的部分和还需要匹配的部分,所以现在这个状态可以写成: $$ T \rightarrow T*\cdot F $$ 也就代表在这个状态下,已经匹配到了$T*$,接下来如果能成功地匹配到一个$F$,就能顺利地归约为栈顶上的一个 $T$。
像这种标记过匹配到的状态的产生式,我们称之为“LR(0)项”,简称“项”。
项集闭包
我们考虑上面说到的 $T \rightarrow T*\cdot F$,以及另外两个项: $$ F \rightarrow \cdot(E) $$ $$ F \rightarrow \cdot \textbf{id} $$
我们可以看到在 $T \rightarrow T*\cdot F$ 项的对应状态下,上面两个项所代表的状态其实就是 $T \rightarrow T*\cdot F$ 在试图匹配 $F$ 时的“子状态”或“等价状态”。
那么我们就把这两个状态和原先的 $T \rightarrow T*\cdot F$ 放在一个集合里面,称之为“ $T \rightarrow T*\cdot F$ 的项集闭包”,其中 $T \rightarrow T*\cdot F$ 称为闭包的核心。
那么项集闭包有啥用呢?我们仍然举上面文法的例子:
比如现在栈中有$...T*$,我们在 $T \rightarrow T*\cdot F$ 状态,我们看到前面有一个$'('$,此时我们就可以根据这个$'('$ 和项集闭包中的$F \rightarrow \cdot(E)$,转到$F \rightarrow (\cdot E)$ 状态,然后去匹配出一个 $F$,放到栈顶,然后进行 $T$ 的归约。
把所有的项、对应的项集闭包以及状态之间的转换关系列出来,我们就可以建立起一个 LR(0) 状态机:
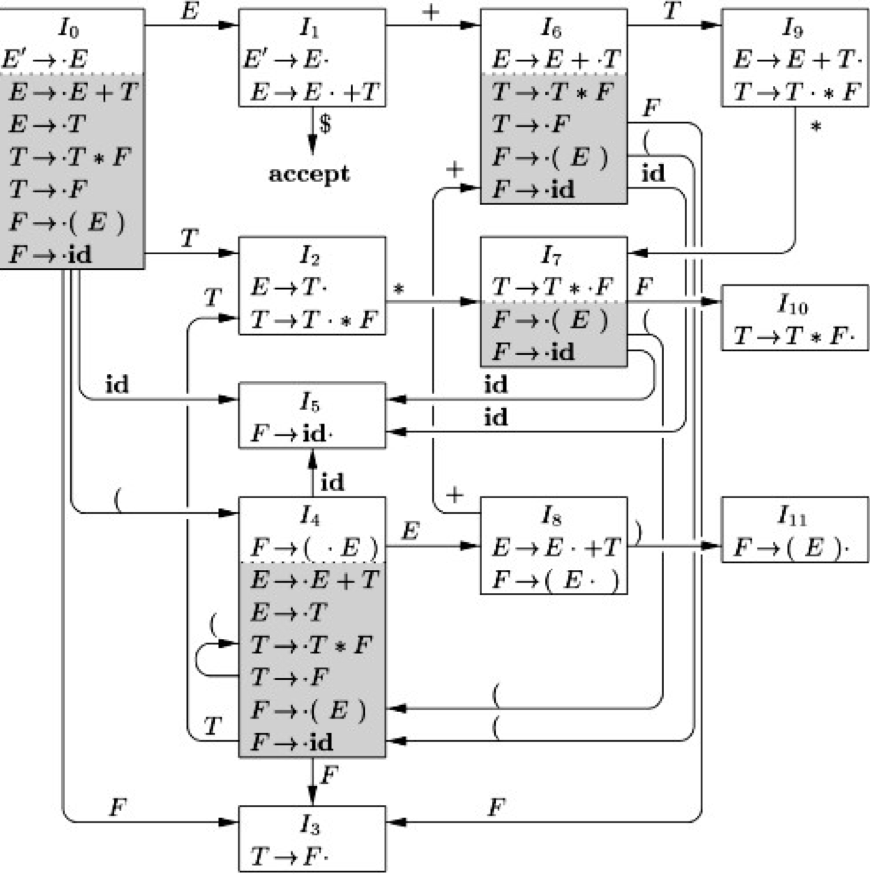
可以看到每一个产生式对应的所有项都会出现在这个状态机里面,而每条边上则指示了在栈顶又被压入某个符号时的状态转换。
其中$E'$是为了标记我们最终匹配到什么而设置的,其实这个例子来讲说到底就是$E$。
上述过程的算法描述
这部分看看就行了,看懂了上面的你可以自己想到这些的。
根据龙书,上面的过程的算法描述为:
-
求每个LR(0)项,直接往所有每个产生式里能插的地方(包括开头和结尾)插入“$\cdot$”即可
-
对开始符号所在的项 $S'\rightarrow \cdot S$,求其闭包
-
寻找每个我们拿到的闭包在某个输入下转换到的项集(称为$GOTO$函数)
-
求法
“If $A → α·Bβ$ is in $CLOSURE(I)$ and $B → γ$ is a production, then add the item $B → ·γ$ to $CLOSURE(I)$, if it is not already there. Apply this rule until no more new items can be added to $CLOSURE(I)$.”
-
-
重复上一步,直到不再有新的项集出现为止
使用 LR(0) 状态机进行匹配
为了存储一路匹配上来时经过的状态,我们需要在分析表中增设一个状态栈。
我不想再画上面那一百万行的巨大表格了,所以我们这次直接用龙书上的例子:
分析$\textbf{id} * \textbf{id}$:
| 状态栈 | 符号栈 | 剩余输入 | 动作 |
|---|---|---|---|
| $I_0$ | $\textbf{id} * \textbf{id}$ | 根据状态机的标识,转到$I_5$(即压入状态栈),同时移进 $\textbf{id}$ | |
| $I_0I_5$ | $\textbf{id}$ | $* \textbf{id}$ | 根据状态机的标识,无处可转,进行归约,弹状态栈 |
| $I_0$ | $F$ | $* \textbf{id}$ | 弹栈后进行下一步状态转移,转到$I_3$ |
| $I_0I_3$ | $F$ | $* \textbf{id}$ | 根据状态机的标识,无处可转,进行归约,弹状态栈 |
| $I_0$ | $T$ | $* \textbf{id}$ | 弹栈后进行下一步状态转移,转到$I_2$ |
| $I_0I_2$ | $T$ | $* \textbf{id}$ | 根据状态机的标识,转到$I_7$,同时移进 $*$ |
| $I_0I_2I_7$ | $T*$ | $\textbf{id}$ | 根据状态机的标识,转到$I_5$,同时移进 $\textbf{id}$ |
| $I_0I_2I_7I_5$ | $T*\textbf{id}$ | 根据状态机的标识,无处可转,进行归约,弹状态栈 | |
| $I_0I_2I_7$ | $T*F$ | 弹栈后进行下一步状态转移,转到$I_{10}$ | |
| $I_0I_2I_{10}$ | $T$ | 根据状态机的标识,无处可转,进行归约,弹状态栈 | |
| $I_0I_2$ | $E$ | 根据状态机的标识,无处可转,进行归约,弹状态栈 | |
| $I_0$ | $E$ | 弹栈后进行下一步状态转移,转到$I_1$ | |
| $I_0I_1$ | $E'$ | 接受 |
注意我这里的步骤比龙书上多了些,龙书将“弹栈后进行下一步状态转移”这一步和下面的步骤合并起来写。
其实说实话你可以把这个状态栈用函数(递归)调用的方法消去的。
冲突
看了上面的步骤你会发现,LR(0) 的每个项集闭包中不可以包含:
-
一个项认为已经可以归约了,另一个项认为还需要移进 $$ A \rightarrow a\cdot b $$ $$ B \rightarrow c \cdot $$
这称为移进-归约冲突。
-
两个项认为可以归约出不同的东西 $$ A \rightarrow b \cdot $$ $$ C \rightarrow d \cdot $$
这称为归约-归约冲突。
有此类冲突的不是LR(0)文法,需要用其他分析方法分析。
这里也可以理解成,匹配完了$E+$ 之后,再递归地(用“干净”的栈帧)匹配后面的以$T*$开头的内容
