有限状态机是能够识别正则文法(正则表达式)的自动机。
确定性有限状态机(Deterministic Finite Automata, DFA)
DFA 包含以下要素:
- 一个有限大小的状态集合,常记为 $Q$。
- 一个有限大小的输入符号集合,常记为 $\Sigma$。
- 一个状态转换函数,其参数为一个状态(设为 $B$)和一个输入符号(设为 $a$),返回一个状态(设为 $C$),表现了状态机在状态 $B$ 时,若接收到输入 $a$,则应该转到状态 $C$,常记为 $\delta$,如 $C = \delta(B, a)$。
- 一个开始状态,常记为 $q_0$,$q_0 \in Q$
- 一个终止或者接受状态的集合,常记为 $F$,$F \subseteq Q$。
DFA 常常用如上五种要素的元组表示,记为 $A = (Q, \Sigma, \delta, q_0, F)$
非确定有限状态自动机 (Nondeterministic Finite Automaton,NFA)
NFA 在 DFA 的基础上,将状态转换函数的返回值从一个状态变成了状态集合,且这个函数的输入参数中,输入符号可以是空串 $\epsilon$。
NFA 确定化
NFA 可以转化为等价的 DFA。
例子
我们从一个例子2开始讲解:
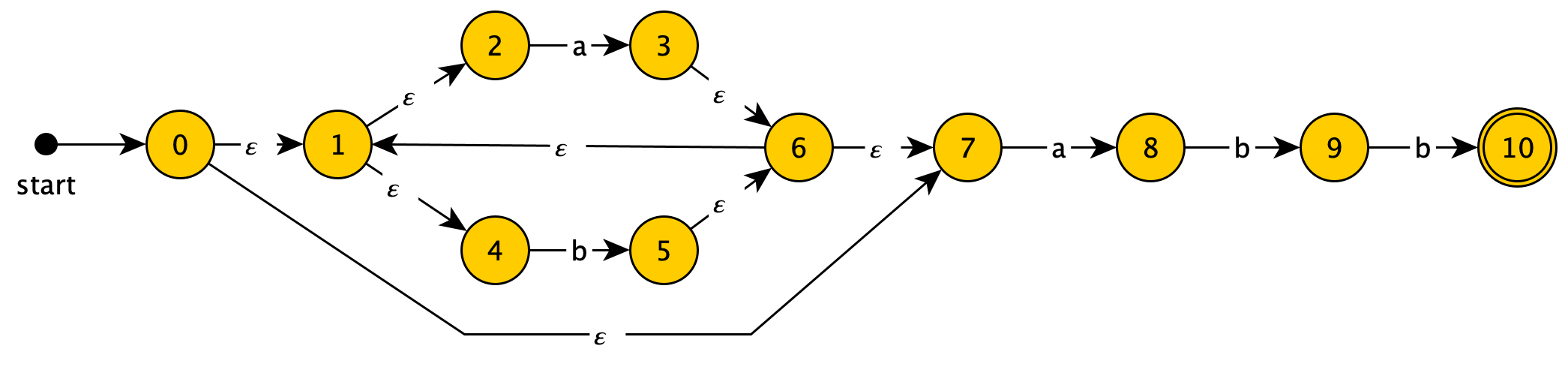
该NFA识别的是$(a|b)*abb$。
我们将这个 NFA 化为 DFA 。
一开始从start进去,即使不作任何输入,从状态$0$开始凭借着$\epsilon$边,也可以转到状态${0,1,2,4,7}$3,那么因为DFA中没有$\epsilon$边,而一个start状态又是必须的,在我们生成的DFA中,这些个状态就只能化为一个状态,称之为$A$。
然后看看我们从这个$A$状态(也就是NFA中的${0,1,2,4,7}$这几个状态)在输入$a$时能转到哪些状态:
- 从$2$,能转到$3$
- 从$7$,能转到$8$
- 从转到的$3$和$8$中,再进行一次$\epsilon$转换(因为这不需要任何输入),能转到${1,2,3,4,6,7,8}$
所以在向原NFA中$A$对应的状态输入了$a$后,可能转到的NFA状态是${1,2,3,4,6,7,8}$,这种组合显然并不是$A$状态,我们把它化为一个状态$B$,并连接在$A$后面:
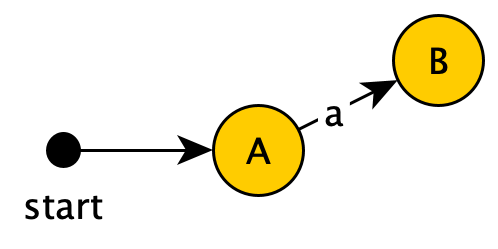
同理从$A$由输入$b$能到达的状态
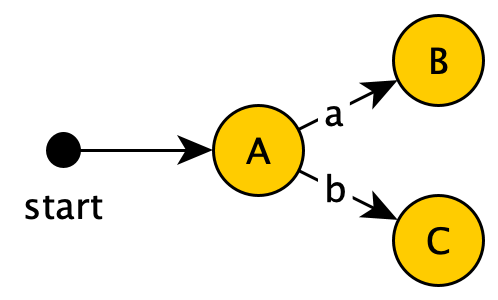
至此从$A$出发的DFA中的路径就考察完了。
为了方便观察,我将NFA中的状态对应到的DFA中的状态标注在图上:
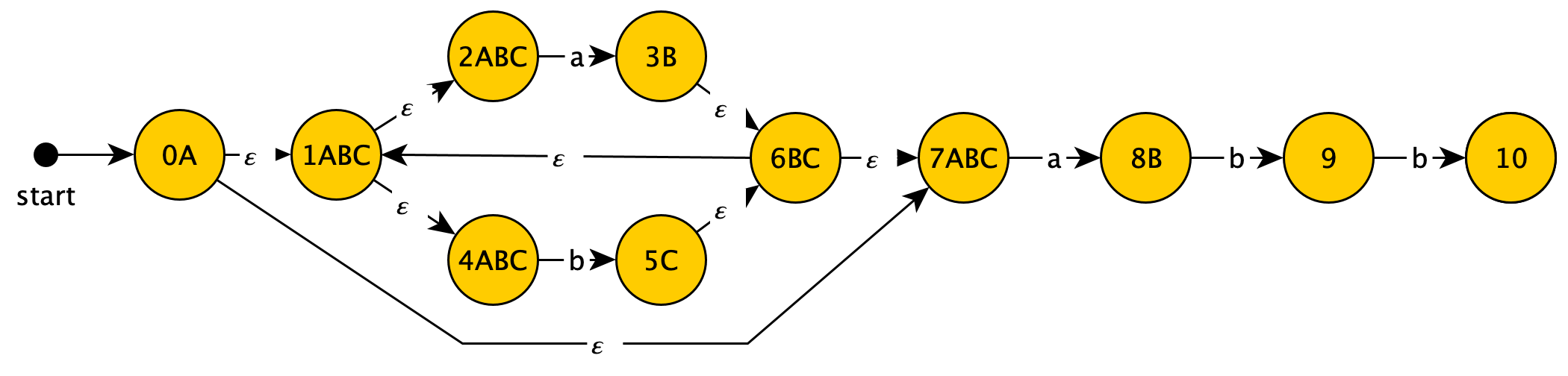
我们继续从$B$开始考察:
- 从这个状态经$a$,可以到达的状态是${1,2,3,4,6,7,8}$,这又落回了$B$,故$B$经输入$a$转到自身。
- 从这个状态经$b$,可以到达的状态是${1,2,4,5,6,7,9}$,这种NFA状态的组合在之前从未出现过,故将其化为一个DFA状态$D$
然后得到:
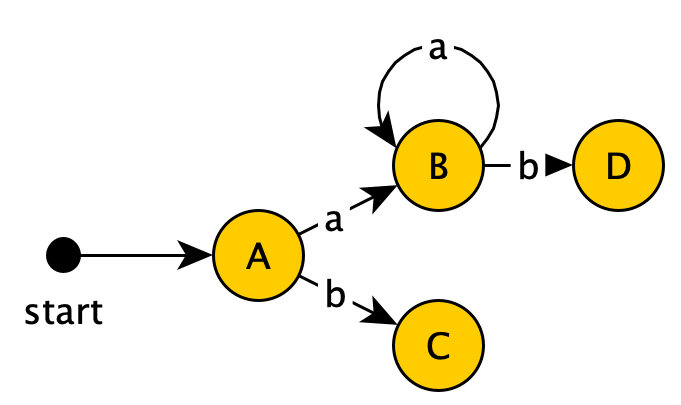
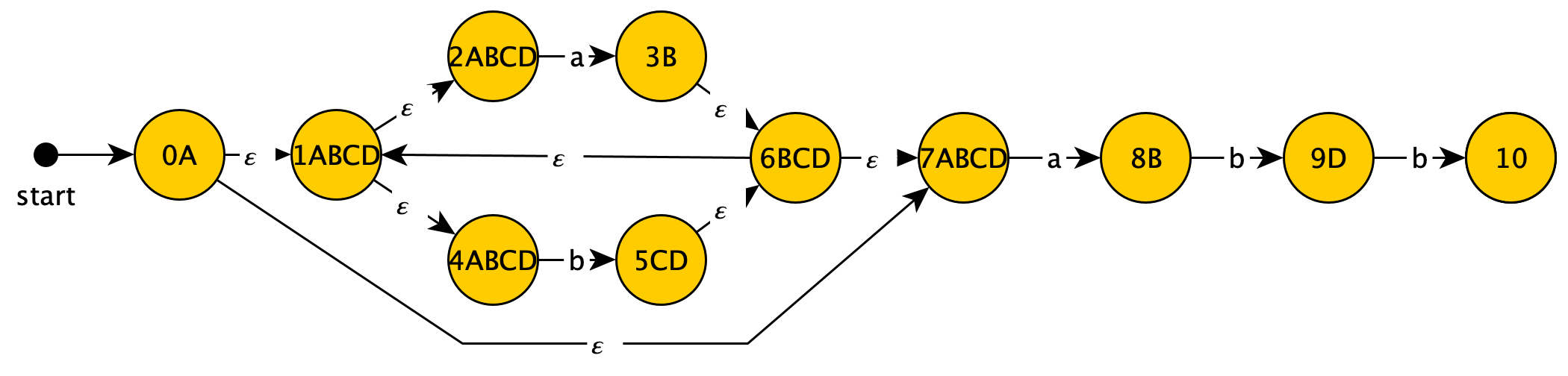
接着考察$C$:
-
$C+a \rightarrow {1,2,3,4,6,7,8}$,落入了$B$
-
$C+b \rightarrow {1,2,4,5,6,7}$ ,落入了$C$
所以:
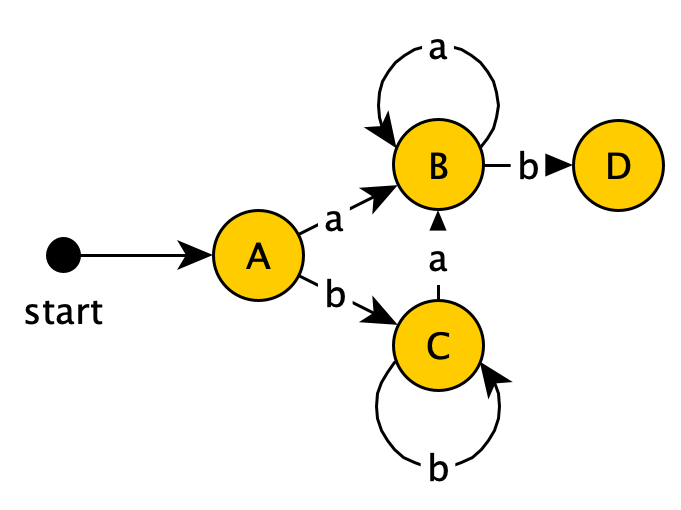
然后是$D$:
- $D+a \rightarrow {1,2,3,4,6,7,8}$,落入了$B$
- $D+b \rightarrow {1,2,4,5,6,7,10}$,创建新状态$E$,由于$E$包含了旧NFA的接受状态$10$,故其是DFA的接受状态。
所以得到:
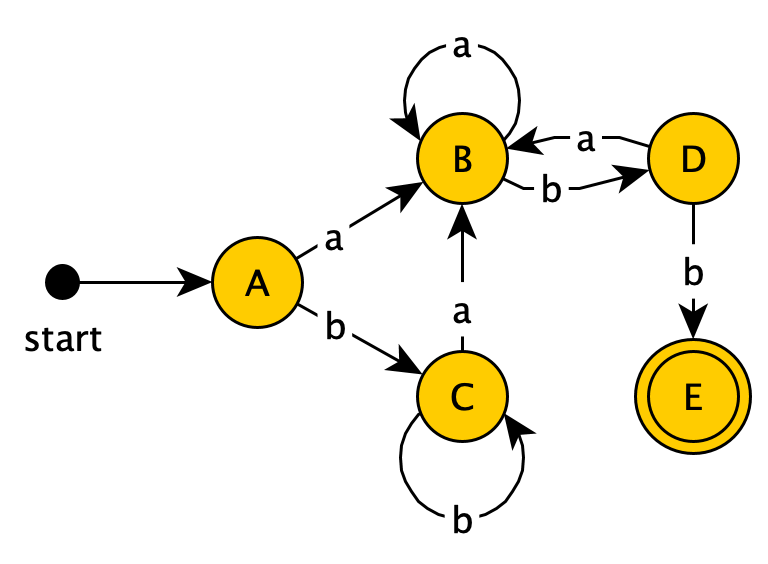

然后是$E$:
- $E+a→B$
- $E+b→C$
所以可以得到:
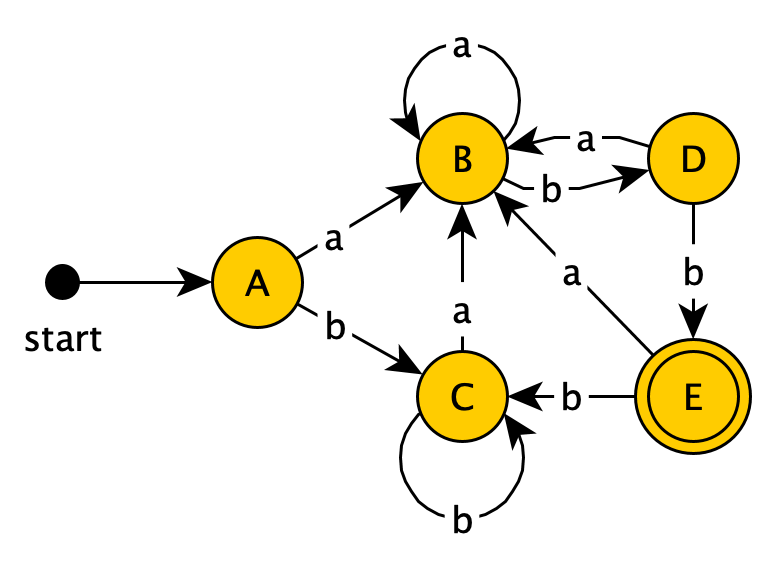
由于这个DFA里面所有的状态都被考虑过了,所以这就是最后的结果了。
附上最后得到的NFA状态到DFA状态的对应关系表:
| NFA | DFA |
|---|---|
| 0,1,2,4,7 | A |
| 1,2,3,4,6,7,8 | B |
| 1,2,4,5,6,7 | C |
| 1,2,4,5,6,7,9 | D |
| 1,2,4,5,6,7,10 | E |
算法
总结上面的过程,我们可以得到NFA的确定化算法:
- 将NFA的开始状态及其所有可通过$\epsilon$边的状态映射为DFA的开始状态
- 如果DFA中的每个状态都被“考虑过”,则算法完成
- 否则,考虑DFA中的一个没有被考虑过的状态$N$:
- 对字母表里的每个字母$ch$
- 找出这个节点对应NFA中的所有节点经过$ch$加上任意多的$\epsilon$边能到达的所有状态的集合
- 若这个集合是DFA中已经存在的某个状态$M$对应的NFA状态集合的子集,则添加连线$N + ch = M$
- 否则向DFA中添加新状态$P$,其对应NFA状态集合就是上述集合,如果这个集合中包含接受状态,那么这个节点也是接受状态,并添加连线$N+ch=P$
- 最终得到的DFA即为所求
代码
代码见Github仓库。
fun toDFA(): Deterministic {
start as Nondeterministic.State
// 还没有被考虑过的状态, equivalentStates: 经过𝜀边能到达的状态
// 由于DFA状态没有完全被构造出来,故存起来比较困难
// 所以存和这个DFA状态对应的NFA状态集
val statesToFind = mutableSetOf(start.equivalentStates())
// 结果的转换关系表
val result = mutableMapOf<Set<Nondeterministic.State>, Deterministic.State>()
var nextChar = 'A'
// 构建DFA开始状态
result[start.equivalentStates()] = Deterministic.State(
nextChar++.toString(),
start.equivalentStates().any { it.accept },
mutableMapOf())
while (!statesToFind.isEmpty()) {
// 现在开始考虑这组NFA状态对应的DFA状态
val theStates = statesToFind.first()
statesToFind.remove(theStates)
for (ch in alphabet) {
val canGoTo = theStates.directConnectedTo(ch)
val equivalenteStates = canGoTo.equivalentStates
// 不存在对应DFA状态,构建
if (equivalenteStates !in result.keys) {
result[equivalenteStates] = Deterministic.State(nextChar++.toString(), equivalenteStates.any { it.accept }, mutableMapOf())
statesToFind.add(equivalenteStates)
}
// 添加该状态到其他状态的转换关系
result[theStates]!!.transitions[ch] = result[equivalenteStates]!!
}
}
// 保存为DFA并返回
return Deterministic(result.values.toSet(), result.values.minBy { it.name }!!)
}
